W = F × d
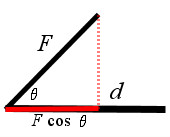 But it's not quite that simple when we start considering vector quantities instead of scalar. When direction enters into it, we have to account for the fact that work can be performed by a force that is not entirely aligned with the direction of the distance traveled. The cosine of the angle of divergence comes to the rescue:
But it's not quite that simple when we start considering vector quantities instead of scalar. When direction enters into it, we have to account for the fact that work can be performed by a force that is not entirely aligned with the direction of the distance traveled. The cosine of the angle of divergence comes to the rescue:W = (F cos θ) × d
Up to this point we have stuck with scalar computations. Vector notation is more powerful and useful. Let's redraw the previous figure in terms of nonparallel vectors F and d. Now we can restate our results.
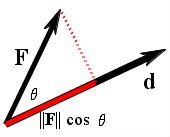 If we use standard vector notation and consider what work actually equals, we end up looking at the following scalar product, which is the parallel component of F times the length of d:
If we use standard vector notation and consider what work actually equals, we end up looking at the following scalar product, which is the parallel component of F times the length of d:W = (||F|| cos θ) × ||d||
This is something we recognize as the dot product of the vectors F and d. In fact, this is probably how the dot product came to be defined as a useful quantity in mathematics. Since we have learned to compute dot products algebraically by multiplying corresponding components and adding the results, we can compute quantities like work without having to compute angles and cosines, making the dot product into something that is easy to compute as well as useful.




No comments:
Post a Comment