A Hallmark moment

Math 342: Problem 7.3.17

It's always entertaining when your teacher gets stuck on a homework problem during a review session for an exam. The problem in question, Exercise 17 from Sec. 7.3, concerns a greeting card company that stashes its cards in two warehouses and wants to ship them as economically as possible to its outlets in San Jose and Memphis. Since I think you're owed a proper explanation of how to solve the problem, let me pick apart the many components of this exercise and try to give you a good and reasonably straightforward solution.

First of all, we're given a broad (and perhaps confusing) hint about what to use as variables. Let's assign them this way: x will be the number of boxes of cards shipped from Warehouse I to San Jose and y will be the number of cards shipped from Warehouse I to Memphis. Since San Jose really wants 350 boxes, it will still need 350 − x boxes (if any) after receiving the shipment of x boxes from Warehouse I. Therefore the balance, 350 − x, must come from Warehouse II. Similarly, since Memphis wants 250 boxes, it will receive y from Warehouse I and 250 − y from Warehouse II.

The object of this exercise is to minimize the total shipping costs in filling the orders from the two stores. We're given this cost grid:


We conclude therefore, that the total cost of shipping the cards from the two warehouses to the two stores will be

z = 25x + 23(x − 350) + 22y + 21(250 − y).

I'm expressing the cost in pennies so as to dispense with the decimal points for now. As we saw in class, when you multiply this out and collect like terms, the object function reduces to

z = 2x + y + 13,300.

Now we need to find a feasible region in the xy plane at whose vertices we can check the object function. Let's list what we know:

Warehouse I has only 500 boxes of cards in stock, so

x + y ≤ 500.

Warehouse II has only 290 boxes of cards in stock, so

(350 − x) + (250 − y) ≤ 290.

When we remove the parentheses and collect like terms, this becomes

600 − x − y ≤ 290,

so

−x − y ≤ −310,

and (dividing by −1 and reversing the inequality)

x + y ≥ 310.

When we graph these two inequalities together, we get two parallel lines and the region between them:


We already know that x and y are both nonnegative, so we care only about points in quadrant I. We must also have 350 − x ≥ 0 and 250 − y ≥ 0 since these are the number of boxes being shipped from Warehouse II. The first condition implies that x ≤ 350 and the second requires that y ≤ 250. When we include these conditions on the graph, we get our feasible region for this problem:


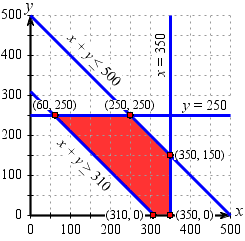
We can now start reading off our vertices. The points (310, 0) and (350, 0) lie on the x axis. The points (350, 150) and (250, 250) are also easy to read from the graph. The remaining vertex lies on the intersection of the line y = 250 with the line x + y = 310. If we plug in 250 for y, we find that x must be 60. Our last point is therefore (60, 250). We can fill in our points and compute the values of the object function at each one:


As you can see, the object function is minimized when x = 60 and y = 250. That means San Jose gets 60 boxes from Warehouse I and 350 − x = 350 − 60 = 290 boxes from Warehouse II, while Memphis gets all of its order from Warehouse I (nothing from Warehouse II). Since we've been expressing the cost in pennies, we should convert it to dollars as we conclude that the minimum shipping cost is $136.70.

Note: This problem could have been done as a four-variable linear programming problem, using the techniques that appear later in this chapter. However, with a creative choice of variables it was possible to solve it with only two variables. That permitted us to do it with a graph in the xy plane. Unfortunately, we won't be going on to those sections of the book that allow us to do more complicated linear programming problems.

Sharon Olson-Hansen

We say goodbye to a dear colleague

It may seem greedy to complain that we had only a year to bid farewell to Sharon, but I'm going to complain anyway. We have been robbed of a dear friend, a cherished colleague, and a great teacher. We are weakened in every way by her loss. The entire mathematics department—the whole college—is in mourning. I can scarcely even begin to imagine the magnitude of the grief among her family members.

Sharon came to us in the fall of 1988 with a full-time faculty appointment for one semester. I knew what she was going through, because I had joined the ARC faculty one year earlier under the same circumstances. When I accepted my appointment, with no guarantee of a subsequent assignment, I had to give up the security of my civil service position in the State Treasurer's Office in a gamble that it would all work out. Sharon made a similar decision about her position as a senior faculty member at Del Campo High School: her seniority and her priority for the best teaching assignments were surrendered when she took the temporary ARC job.

When Sharon arrived, I had just won my wager and was beginning a new tenure-track appointment. She was not quite as lucky. There was no assignment available for her when her fall semester appointment expired. Sharon was reduced to a part-time teaching position during the spring, but she hung in there, hoping that a new opportunity would present itself for fall. Fortunately, new positions were approved for fall semester for the math department and we snatched her up for a full-time appointment. It has always been a particular point of pride with me that I was on the hiring committee that sent Sharon's name to the college president as a finalist for a permanent faculty position. It was one of the best decisions we ever made.

During her years of full-time service on the ARC math faculty, 1989-2005, Sharon demonstrated how important one determined and dedicated person can be even in a large organization. She was a tireless worker on behalf of her colleagues and her students. She served as department chair, a position with plenty of responsibilities and minimal benefits, requiring both an attentive ear and diplomatic skills. Her success in the position was so great that people were always trying to talk her into a second term, but she wisely resisted. Besides, she was busy with her work on the college's facilities, making sure that our planning process was fully informed of the practical needs of instructors and students, the people who actually occupied and used those facilities. Sharon chaired the committee that drafted the facilities chapter of the college's accreditation self-study, making a significant contribution to the excellent evaluation ARC later received from the visiting accreditation team.

Sharon was an early supporter of our highly speculative plan to put Howard Hall in our educational master plan, back in those days when no such building was even on the drawing board. When the college administration revealed an initiative to construct a new faculty office building on campus, we were first in line with our documented need for a new facility. (And, yes, we did succeed in getting it named “Howard Hall,” after our late dean and vice president of instruction.) We're going to miss having Sharon's help in facilities planning as the renovation of the campus center looms on the horizon, but we'll do our best to remember her lessons and dedication. It will be so much more difficult without her.

Some of Sharon's students planned to try to get Sharon the Instructor of the Year award during the 2005-06 school year. They were going against the odds, of course, nominating an instructor who was gone from the campus and fated never to return, but it was a noble and kind gesture by students who were devoted to their teacher. In truth, it should have been only a matter of time before Sharon was properly recognized as one of the college's most skilled and thoughtful instructors. The loss to our students is as great as the loss to colleagues and campus. One of our small comforts is the thought that Sharon's students are part of her legacy, and their experiences with her will last throughout their lives.

The spring of 2005 was difficult for Sharon. She never felt entirely well and the cause was eventually traced by her doctors to a gall bladder problem. Or so they thought. She had the gall bladder removed at the end of the school year and returned to the classroom for the 2005 summer session, but her problems continued. The doctors began to suspect liver problems. She turned her summer session class over to a substitute and continued her search for a definitive diagnosis and treatment. On June 29, I ran into Sharon and her son Ryan at a local Davis restaurant and she invited me to join them for lunch. She was in a festive mood, telling me they had just received good news on her prognosis: the liver problem was manageable and she was greatly relieved. Later she told me that false hope had given her and her family their happiest day after weeks of worry.

Immediately thereafter she learned the doctors had been wrong in their optimistic assessment. Sharon composed a message to her math department colleagues, sharing the bad news. We were all aghast to learn she had inoperable pancreatic cancer, but she was determined to fight it long enough to see her sons graduate from school: Colin from San Diego State in December and Ryan from Da Vinci High School in June. Despite the long odds, she succeeded, as those who knew her always believed she would.

Let me leave the last word to Sharon herself, from her message to her colleagues back in July 2005:

---

I want you all to know, that I have always been so proud to be a part of this department. This is not some PR statement. I am always bragging about what a great job I have and what fascinating people I work with from faculty, to clerical and management staff, and all the other support staff—tutors, IA's, computer techs, ... Teaching gave me a sense of satisfaction that I am desperately going to miss. I loved those “Ohhhhh!” moments from students, and I told them that those were what I went into teaching for. I will miss the camaraderie in the halls, the razzing at department meetings, Brother Oliver's on Fridays, department parties, walking to class with whoever, my new little decorated office with a clean bathroom down the hall!, and so much more. You have been my family for 17 years, and I will miss all of you. But I know you will continue to make this department one of the best places for students to come and learn what we all know is the beauty of math.

I am forever thankful to have been a part of that, and I love you all dearly.

—Sharon

---