We will spend a lot of time on names and procedures. We learn the names of things as part of identifying what we are working on. Once we know what we have, then we apply the appropriate procedure to transform it into an answer or simplified result.
The main goal of elementary algebra is to give everyone the ability to work with quadratics (any anything simpler). At the end of the semester you should be comfortable with quadratic expressions like ax2 + bx + c, where "quadratic" refers the to square in x2 ("x squared"). Sometimes we like to give a quadratic expression a name and call it a quadratic function. Our favorite function name is f and the notation we use is
f(x) = ax2 + bx + c.
If we set a quadratic function or quadratic expression equal to zero, we have a quadratic equation:
ax2 + bx + c = 0.
Now the big question is, what values of x will make the equation true? The good news is that a formula exists to provide us with all the answers. It's called the quadratic formula (what a surprise). The bad news is that it will take us a while to get there and a lot of work will be required of us. Still, here is the results we're after, the quadratic formula:
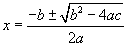 We'll be working out the details as we go along.
We'll be working out the details as we go along.



